Faktoriyel Sorusu (Baba Sorulardan)

   3 . 1 !  +  7 . 2 ! + 13 . 3  ! + 21 . 4 ! + ...... + 2971 . 54 !  toplamının sondan kaç basamağı 9 dur?


Bu soruda  ben çözüm için ilk aşama olan düzenleme yazacak olursam oda şöyle,

( x ^ 2 + x + 1 ) . ( x ! )  şeklinde olmalı
x 1 den 54 e kadar ,
sonrasında takılmamız gereken yer . yardımcı imkanı olursak mutlu sonla sevinirim.

Üstad  işi olarak parantez içine x ekleyip çıkarırsak ( x + 1 ) . ( x + 1 ) !  -  x . x !   gelir.

Sanırım oradan bir şeyler ortaya gelir.

 55 ! - 1  olur ki sondan 13 basamak 9 dur.
değerli soruda güncelledikten sonra çözüm aşamalarını ilerler ama

55 . 55 ! - 1 haline getirmek zaman alır .

Şimdi . bu arada genel terimi sonlu farklar yöntemi ile bulmuştum.

8 ile Bölünebilme Sorusu

Bölünebilme kurallarını hatırlayalım.

2 ile bölünebilme kuralı : Birler basamağı 2 nin katı olmalı idi. (abcd sayısında d alınır.)

4 ile bölünebilme kuralı : Birler ve onlar basamağı 2 nin katı olmalı idi. (abcd sayısında cd alınır.)

8 ile bölünebilme kuralı : Birler, onlar ve yüzler basamağı 2 nin katı olmalı idi. (abcd sayısında bcd alınır.)

Soru : ab13 dört basamaklı sayısının 8 ile bölümünden kalan x ise x kaç farklı değer alır?

Bu soruyu deneyerek bulunabilir. Deneme yaparak çözüm yapmak uzun sürer. Yorum yapmak gerekirse
 k l  a s i k  çözüm ile sonuca ulaşabiliriz.


Çözüm : b13 e bakacaz.

100b+13 = 4b+5 ( mod 8 )
 b çif iken kalan 5 dir

b tek iken  4 ( 2 n - 1 ) + 5 =  1  ( mod8 ) yani kalan 1 olur,

Bu durumda x değeri 1 ile 5 olup 2 farklı değer alabilir. Şeklinde bir çözüme sahiptir.

Kitapların Ygs'yi Tutturması

Merhaba, bir öğretmen olarak sizlere kitapların Ygs'yi tutturma durumunu ele almak istiyorum. Buradaki kitaplar hem MEB'in dağıttığı kitaplar hem tavsiye edilen kitaplar hem özel yayınlar ile ilgili.

Ygs'de ders kitaplarından soru gelme olayı

Bu konuda ne düşündüğümü ifade etmek istiyorum.

2012 yılında önce fizik dersi  Lys sorularının  30 sorusunun 13 tanesi aynısı yani bire bir tıpa tıp gelmişti.

2014 yılında Ygs matematikte özellikle bu yıl AYDIN yayınları gelmişti

 Aydın yayınları kitapları çok bilgi yüklü kitaplar ve detayı çok fazla ele alıyorlar.

2015 yılında yani bu yıl 12. Sınıf kitabının en arkadaki

Ünite Değerlendirme

 sorularına dikkat etmek lazım

Matematik dersinde en başarılı yayınlardan biri Ekstrem yayınlarının çıkardığı kitaplardır. Adana ilinde özel bir dershane hatta okul aşamasında olan Ekstrem yayınları sahibi Celal İŞBİLİR de kendisi hayatını eğitime adamış bir eğitmendir.Sadece matematik kaynakları değil fizik, kimya, biyoloji ile Türkçe, tarih, coğrafya ve felsefe kitapları da çok faydalı eserler arasında yer alır.

Sayı Sorusu (Asal Sayı)

Bir sayı sorusu ile beraberiz. 

x, y ve z asal sayılar olmak üzere, x . z = 7 + x . y olduğuna göre, y + z - 2 x ifadesi kaça eşittir?

Soru asal sayı ile ilgili ve şık ve kolay bir sorudur. Keyif alınacak hoş bir sorudur.

Bu arada farklı sorular ile jimnastik tekniği uygulayarak geleceğe bir adım daha atmaktayız. her adım bizi ileriye götürecektir.

x, y ve z asal sayılar olmak üzere, x . z = 7 + x . y olduğuna göre, y + z - 2 x ifadesi kaça eşittir?

x . z = 7 + x . y

x . z - x . y  = 7

x . ( z - y ) = 7

x = 7 , z = 3 ve y = 2 olur.

x . z = 7 + x . y işleminde direkt değer vermeyi de düşünebilirsiniz. Değer verme de biz çözüm yöntemidir.

Basamak Sorusu Şık Bir Soru

Ygs sınavı sayı basamakları konusuna aittir. Basamak sorusu oldukça şık bir soru sunacağım size bazı dershanelerin M1 bazılarının F1 dedikleri sınıflardaki yaprak testlerden seçtim. Bu soru sıradan değil zor değil ama basit de sayılmaz. İşin ilginç yanı bazen kolay soruyu zor testte koymaktır.

m < n < k  olmak üzere mnk üç basamaklı dört tane farklı doğal sayısının toplamı 1191 olduğuna göre bu şartı sağlayan mnk üç basamaklı sayıların en büyüğü en az kaçtır? Soru budur.

Çözümü inceleyelim.

Çözüm : mnk üç basamaklı üç  tane farklı doğal sayısı seçelim. En büyüğü en az dediği için 1191 sayısının 4 ile bölümünden 290 civarı sayılar seçilir.

278 + 279 + 289 + x = 1191 olup  x = 345 çıkar.

Sorularda tek tek yazalım. En büyüğü en çok kaç farklı en büyüğü en az farklıdır. Biri en azları yazarken diğeri ortada yazar. S o r u y u iyi okuyun.

9. Sınıf Kümeler Ödevi

2014 - 2015 sezonunda 9. sınıfta  matematik dersinde kümeler konusu ile ilgili ödev hazırlarken bazı noktalara dikkate etmek lazım.

Küme tanımı  (1 saat, 1 gün, en az 10 soru ve çözümlü örnekler)
Faktoriyel (1 saat, 1 gün, en az 5 soru ve çözümlü örnekler)
Küme Gösterimi (2 saat, 2 gün, en az 15 soru ve çözümlü örnekler)
Problemler  (4 saat, 4 gün, en az 100 soru ve çözümlü örnekler)
Kombinasyon (1 saat, 1 gün, en az 5 soru ve çözümlü örnekler)
Çıkmış sorular(7 saat, 7 gün, en az 150 soru ve çözümlü örnekler)
Küme teoremi (2 saat, 2 gün, en az 20 soru ve çözümlü örnekler)
Çözümlü sorular (1 saat, 1 gün, en az 50 soru ve çözümlü örnekler)



Lys konuları da sıralama değiştireceğe benziyor kümelerden de bir soru olabilir nerede kaldı polinomlar ile başlayıp çarpanlara ayırma, ikinci dereceden denklemler diye devam eden ikinci dereceden eşitsizlikler, ikinci dereceden fonksiyonlar limit yani eski adıyla Öys der gibi insan.

10. Sınıf Değişiklik

2014 - 2015 sezonunda matematik dersinde ciddi değişiklikler oldu çok konu sadeleşti bazı konular eklendi sıralama farklı ilk konu eski sistemin tamamen kalktığını devletin yavaş yavaş teog sistemine geçeceğini az az haber veriyor gibi.ilk dönem

sayma  (2 saat, 2 gün, en az 20 soru ve çözümlü örnekler)
faktoriyel (3 saat, 2 gün, en az 30 soru ve çözümlü örnekler)
sıralama ve seçme (1 saat, 1 gün, en az 5 soru ve çözümlü örnekler)
permütasyon (3 saat, 2 gün, en az 40 soru ve çözümlü örnekler)
kombinasyon (1 saat, 2 gün, en az 10 soru ve çözümlü örnekler)
pascal üçgeni (1 saat, 2 gün, en az 10 soru ve çözümlü örnekler)
binom teoremi (3 saat, 2 gün, en az 40 soru ve çözümlü örnekler)
koşullu olasılık (3 saat, 2 gün, en az 40 soru ve çözümlü örnekler)

konuları var eski sistem sil baştan denilmeye çalışılıyor.

Lys konuları da sıralama değiştireceğe benziyor nerede kaldı polinomlar, çarpanlara ayırma, ikinci dereceden denklemler, ikinci dereceden eşitsizlikler, ikinci dereceden fonksiyonlar yani parabol der gibi insan.

Küme Sorusu (Yöntem Yayınları)

Küme sorusu yöntem yayınlarında çıkan bir kitaptan çok beğendiğim için sizlere sunuyorum. Soru bana
o r i j i n a l geldi.

A = { 1, 2, 3, ... , 8 } kümesinin 3 elemanlı alt kümelerinin kaç tanesinde, 6 ait olduğu kümenin en büyük elemanıdır?




C ( 5, 1 ) + C ( 5, 2 ) mi alınacak diye düşünebiliriz.

Şimdiden teşekkürler 1, 2, 3, 4 ve 5 elamanları arasından seçilecek elamanlar

C(5,2) olmalı

 tek kelime yazacağım NEDEN?

 6 kesin olacaksa yanına 2 elemanı 6 dan küçük 1, 2, 3, 4, 5 arasından seçeriz diye düşündüm

 6 illa olacak mı ?
 6 kesin olmadan bulunduğu kümenin en büyüğü olamaz zaten.
10 olmalı.
 :-)))) :)))  :) :-))))

 Burada ilginç olan sayılar yazılırken dikkat etmek lazım en büyük sayı 6 olacaksa 7 ile 8 olmaz geriye 6 da iki kere yazılamayacağına göre, bir, iki, üç, dört ve beş yazılır.

Ygs Temel Kavram Sorusu

Matematik derya deniz bir ders olup her soruya ayrı bir itina ile yaklaşılmalı.

Bir değişik soru ile size bir bakış açısı kazandırmaya çalışalım. Bu sorular çok tatlıdır. Çözmesi çok keyif verici olur. Bu soruları can simidi saymalı ve kaçırmamalı. Temel kavram soruları iyi bellenmeli.

a asal sayı diyor. 2, 3, 5, 7, 11 gibi sayılardan bahsediyor. Asal sayı olduğu için ras gele bir s a y ı alınmaz.

a = 5b + 6 / b bu işlemi yaparak b nin kaç farklı değer alacağını bulalım. Bu işlemde işler çarpımı ve parantez gelecektir.

a b = 5b + 6           5b yi karşıya atalım.

a b - 5b = 6

b (a - 5) = 6

b = 6 / a-5 

a yerine 2, 3, 7 ve 11 gelirse 

b değeri - 2, - 3, 3 ve 1 değerini alır. b nin 4 değeri olur. Böylelikle bir soru daha çözdük.

Kümeler (Eksen Baba Testten)

Küme sorularında çetrefilli kelimelere dikkat ediniz.Bazen çok basit bir soru zor gibi görünebilir.

A = { a, b, c, d, e, f, g } ve   B={ 1, 2, 3, c, d } olduğuna göre A U B kümesinin 4 elemanlı alt kümelerinden kaç tanesi A kesişim B kümesini kapsar ? Ne kadar basit aslında baba test olduğuna aldanmayın.

Burada  A = { a, b, c, d, e, f, g } ve   B={ 1, 2, 3, c, d } kümeleri için A U B kümesini bulalım.Bu basit bir işlem zaten.

A U B = A = { a, b, c, d, e, f, g } U   B={ 1, 2, 3, c, d }=  { a, b, c, d, e, f, g, 1, 2, 3 }olur burada kesişim kümesi 2 elemanlı olup { c, d }dir. Şimdi 10 elemandan iki elemanı çıkarın.

Kombinasyon ( 8 , 2 ) olacağı için 8 . 7 / 2 den 28 çıkar.Hepsi bu kadar.

Faktoriyel Sorusu

145! sayısının sondan kaç basamağı sıfırdır? Tip sorularını cevaplayalım.

Bu sorularda maksat faktoriyel içinde aynı asal çarpandan kaç tane olduğunu bulmaktır.
Diyelim ki 10! sayısında kaç tane 2 çarpanı olduğunu soralım. 10! = 1 . 2 . 3 . 4 . 5 . 6 . 7 . 8 . 9 . 10 olduğundan çift sayıları alalım. 2 de 1 tane 2 çarpanı, 4 de 2 tane 2 çarpanı, 6 de 1 tane 2 çarpanı, 8 de 3 tane 2 çarpanı, 10 da 1 tane 2 çarpanı olmak üzere 8 tane 2 çarpanı vardır ya da 10 da 2, 5 kere ; 5 de 2, 2 kere ; 2 de 2, 1 kere var deriz ve 8 tane 2 çarpanı buluruz.

145! sayısının sondan kaç basamağının 0 olduğunu bulmak için 5 ile böleriz.

145 de 5, 29 kere ; 29 da 5, 5 kere ; 5 de 5, 1 kere vardır. Yani 145! sayısının sondan
29 + 5 + 1 = 35 basamağı sıfırdır

Mental Aritmetik

Mental aritmetik hakkında biraz sohbet edelim.

Son günlerde ( son 4 yıldır nerdeyse ) oldukça popüler olan hatta tüm televizyon kanalarındaki yetenek yarışmalarında da fazlasıyla ilgiyle karşılaştığımız süper zeka olarak nitelendirilen ya da öyle bir algı oluşturulan  çocukların aldığı mental aritmetik eğitimini biraz irdeleyeceğiz.

Peki gerçekten bu  mental aritmetik öğrenci için faydalı bir eğitim midir?

Tabi ki hayır. Öncelikle bu konuda oldukça araştırma yaptım.

Nasıl eğitim veriliyor? Akademik temelleri nelerdir?

Öncelikle burada şu soruyu özellikle sormalıyız kendimize:

Matematik bilmek nedir?

Matematik bilmek, üç beş soruyu çok hızlı zihinden yapma sanatı, yapma becerisi değildir. Kesinlikle mental aritmektikte çocuklara zihinlerinde canlandırmaları için bir abaküs veriliyor. Bu abaküste nasıl dört işlem yapacakları anlatılıyor. Çocuklar bunları askeri bir disipline benzer sınıf ortamlarında ezberliyorlar. Daha sonra bu çocuklara 20 tane iki basamaklı sayı veriliyor ve hadi topla deniliyor. Çocuklar bu toplama işlemini zihinlerindeki abaküsün boncuklarını aşağı ya da yukarı hareket ettirerek hesaplıyorlar. Abaküsün son durumundaki halinin sayısal karşılığı neyse sonuç o oluyor.

Temel Kavramlar (Baba Soru)

Temel kavramlar konusu Ygs hazırlıkta ilk konu olup soru sayısı çok geniştir. Bazı sorular yazılırken hiç dikkat edilmez ta ki çember analitiği sorusu temel kavramlar testi içine kadar girer. Bu da öğrenciye itici gelir öyle ki öğrenci ilk konuyu bile yapamıyorum diye düşünmeye başlar.

mesela şu soru esasta çember analitiği sorusu olmasına rağmen Ygs matematik kitabında ilk testte yer almış. 

x ve y doğal sayılar olmak üzere, x . ( x + 4 ) küçük veya eşit ( 3 - y  ) . ( 3 + y ) eşitsizliğini sağlayan kaç tane ( x , y ) ikilisi vardır?

parantezleri dağıtalım 

( x + 2 ) nin karesi + y nin  karesi küçük veya eşit 13

x = 0 için y = 0, 1, 2, 3 değerlerini alır.

x = 1 için y = 0, 1, 2 değerlerini alır.

toplamda 7 ayrı ( 0 , 0 ),  ( 0 , 1 ), ( 0 , 2 ), ( 0 , 3 ), ( 1 , 0 ), ( 1 , 1 ) ve  ( 1 , 2 ) doğal sayı ikilisi vardır.

Değer Bulma (Baba Soru Tarzı)

Ygs matematik temel kavramlar kısmı ile ilgili değer bulma sorularından baba soru tarzı bir soruyu sizlere anlatmaya çalışacağım. Bu soruyu sadece çözmeyeceğiz aynı zamanda yol göstereceğiz genelleme üzerinden.

Bir kere soru modeli a + b = k ise bu soruyu nasıl genelleyebiliriz  diye düşünelim. 

Burada k sayısı önemli değildir. k yı eşit ik parçaya bölüp çıkan (eşit) iki sayıyı çarptığımızda çıkan sonuç maksimum değerdir. Burada sanki aritmetik ortalama ve geometrik ortalama arasındaki ilişkiden çıkması gibi bir durum da vardır.

 İşlem TAMAMDIR HOCAM dersiniz siz de soruyu bu mantıkla çözebilirsiniz.

Çözüm  oradan geliyor. 

 x ve y eşit olsa  x . y çarpımı maksimum yani en büyük değer alır x ile y yi çarpmalarının bu durumda 1/100 olmasi gerektir.  ( x = y = 1/10 ) cevapta 1/100 den küçük olmalıdır. 1/96 olamaz.

Siz de bu p r a t i k çözümü kendi başınıza kağıda biraz bastırarak yazın ve başka örnekler üzerinde uygulayın. k eşit iki parçaya ayrılacak.

Temel Kavramlar En Büyük Değer

Ygs matematik çözülmesi gereken hatta lys tipi temel kavram sorularından şık bir soru ile sınava hazırlık yapan öğrencilere güzel bir çözüm vermeye çalışacağım. Bu çözümü dikkatli izleyin ve iyi belleyin.

A, B ve C pozitif tam sayı ve A > B > C olmak üzere, A + B / C = 23 olduğuna göre, A + B + C  toplamının en büyük değeri kaçtır ?

A > B > C  ise B / C > 1 olur. Her iki tarafa A eklersek 

A + B / C > A + 1 den

A + 1 < 23 ve 

A < 22

A nın en büyük değeri 21 olur ve B = 2 C olur.  B = 20 C = 10  olur.

Anahtar kelime sıralamadır. A, B ve C sayılarına değer verilip de çözülür ama sayılar büyüdükçe çözüm zor bir hal alır. Yazın ve tek tek adım adım yazın çözüme ulaşın.

Alt Küme Şık Soru

Ygs konusu ve 9. sınıf matematik konusu olan kümeler ile ilgili alt konularından alt küme ilgili çok güzel sorular vardır. Bu sorular yer yer çok ağır olabilir bazen soruya nerden başlanır çıkartmak zordur. Bunun emsali olan sorulardan bir tane sunmak istiyorum. Soruyu dikkatle çözün ve sonucu bulun. Ayrı bir yere not alın.

Sorumuz alt küme sayısı ile ilgili bir soru ve çözümü de çok hoş. Güzel soru yazan ellere kuvvet.
Birbirinden farklı n tane kümenin alt küme sayıları toplamı 1000 dir.
Buna göre, bu kümelerden eleman sayısı en az olanı kaç elemanlıdır?


2^n icin
1.küme 9 elemanlı 512
2. küme 8 elemanlı 256
3. küme 7 elemanlı 128
4. küme 6 elemanlı 64
5. küme 5 elemanlı 32
 6. küme 3 elemanlı 8
Toplam 1000
 En az 3 elemanlıdır.

Tek tek saymak zor olur ama çok da uzun sürmeyecek bir soru modeli. Bu soruyu 2 nin farklı kuvvetleri toplamı nasıl 1000 eder diye de sorulabilirdi.

Kökler Toplamı Baba Sorulardan

     Ygs ile Lys karışımı sorular vardır. 

     Yukarıda verilen soruyu önce doğru teşhis etmemiz gerekir. Zira soruyu doğru anlamak bizi sonuca götürür. Bu sebeple doğru ve dikkatli okumalıyız.

     Hem temel kavramlar sorusu hem ikinci dereceden denklemler sorusu ile ilgileneceğiz. Soru ilk okunduğunda temel kavramlar sorusu şeklinde anlaşılır. Fakat işin içerisine ikinci dereceden denklemlerin kökünü bulmadan kökler toplamı da devreye girmektedir.

     İlk önce ifadeyi sağ tarafı sıfıra (0) eşit olan bir kapalı denklem haline getirmemiz gerekir. Ondan sonra kök toplamını bulmak için kökler toplamı formülünü kullanabiliriz. 

     Çözüme dikkat edersek önce kesirden kurtarıyoruz. Tüm değerleri sola taşıyarak sağı 0 (sıfır) a eşitliyoruz. Burada ikinci dereceden bir ifade ile karşılaşmış oluyoruz. Kökler toplamı formülünü bilmemiz gerekir. Burada zaten anahtar ifade kökler toplamıdır.

    Bu tür sorularda yazarak çalışmak bir kere iki kere yazmak yeterlidir. Siz bu tür soru için hem fikir hem yorum gücü kazanmış olursunuz. Yazarak çalışmak öğrenmenin en sık olarak kullanılan yöntemidir. Yazın.

Faktoriyelde Bölen Sayısı

Ygs matematik konularından temel kavramlar bölümünün sonunda faktoriyel işlemleri vardır. Bu işlemler bazen çok karmaşık bazen çok uzun gibi gelir. Sorumuz faktöriyelde bölen sayısı ile ilgili.

13! sayısının pozitif tek bölenlerinin sayısı kaçtır ?

Sorumuzda tek çarpan istediği için asal çarpanlardan 3, 5, 7,  ... gibi çarpanlar lazım olacak.

13 sayısının 3 ile böldüğümüzde 4, 4 ü 3 e böldüğümüzde 1 kere var yani 3 olan tek çarpanı 5 tanedir.

13 sayısının 5 ile böldüğümüzde 2 kere var yani 5 olan tek çarpanı 2 tanedir.

13 sayısının 7 ile böldüğümüzde 1 kere var yani 7 olan tek çarpanı 1 tanedir.

13 sayısının 11 ile böldüğümüzde 1 kere var yani 11 olan tek çarpanı 1 tanedir.

13 sayısının 13 ile böldüğümüzde 1 kere var yani 13 olan tek çarpanı 1 tanedir.

Çarpan sayılarının 1 fazlasının çarpımını alalım.

( 5 + 1 ) . ( 2 + 1 ) . ( 1 + 1 ) . ( 1 + 1 ) . ( 1 + 1 )   = 6 . 3 . 2 . 2 . 2 =  144

Ygs Kelime Oyunu

Ygs kelime oyunu hakkında biraz sohbet edelim. Bazı sorularda ilk okunuşta yanlış anlaşılır ve öğrenci hemen cevabı bulduğunu sanır. İki ayrı sayı vardır ve sizi yanlış yorumlamaya iter ve bundan dolayı dikkatli okumak gerekir. Aşağıdaki örnek buna çok uygundur.

Rakamları farklı ve çift olan 3 basamaklı en küçük pozitif tam sayı rakamları farklı iki basamaklı en küçük pozitif tek sayıdan kaç fazladır ?

Ne kadar basit değil mi hemen 102 - 13 = 89 der ve sevinirsiniz. Otur yerine 0. Aaaa deyip şapa oturursunuz. Kelime oyunu var. 

Rakamları farklı ve çift olan 3 basamaklı en küçük pozitif tam sayı 102 değil 204 olacak.

İkinci sayı için bir sorun yok. Onun için de oluşturulabilirdi.

Cevabımız : 

Rakamları farklı ve çift olan 3 basamaklı en küçük pozitif tam sayı rakamları farklı iki basamaklı en küçük pozitif tek sayıdan 204 - 13 = 189 fazladır. Soruyu bir de siz çözün. Yazmak en etkili yoldur.

En Büyük Değer Sorusu

Ygs matematik sorularından değişik bir en büyük değer sorusu ile devam edelim. Bu tür soruları çözmek size düşünme gücü katar. Yorumlama yeteneği kazandırır. 1, 2, 3 derken netleriniz bakmışınız artmış.
Soru şöyle :

a ve b birer pozitif tam sayı
a . b = 2a + 10 olduğuna göre, a kare -  b  ifadesinin en büyük değeri kaçtır?

a . b = 2a + 10     2a ifadesini sağdan sola taşıyalım.
a . b - 2a  =  10    a parantezine alalım.
a . (b - 2) =  10    burada değer verebiliriz.

a için 10 ve b için 3 alırsak eğer a kare -  b  ifadesinin en büyük değerinin bulunması için en büyük olması için n en büyük b en küçük olmalıdır. a kare -  b  ifadesinin en büyük değeri  : 10 un karesinden 3 çıkınca sonuç 97 olarak bulunur. Siz de bakmadan çözün ve bulun. Olmadı tekrar baştan başlayın ve bulun.

http://www.sketchtoy.com/63010290

Aralarında Asallık

Testlerde aralarında asallık ile ilgili pek çok soru vardır. Sayı küçük olursa tek tek sayılır ama sayı büyüdükçe saymak zorlaşır.

12 ile aralarında asal ve 12 den küçük doğal sayıları bulalım.

Bir kere sayımız çift olduğu için çift sayılar ile aralarında asal olamaz. O zaman 2, 4, 6, 8, 10 sayıları elenir. 12 sayısı 3 ile bölündüğü için 3 ün katları ile de aralarında asal olamaz. O zaman 3 ve  9 sayıları elenir. 6 da 3 ün katı ama sayıyı çift kategoride eledik zaten. Geriye 1, 5, 7 ve 11 kaldı demek ki  12 ile aralarında asal ve 12 den küçük doğal sayılar 1, 5, 7 ve 11 olur.

48 ile aralarında asal ve 12 den küçük doğal sayıları bulalım.

Bu sayıları tek tek yazacak olursak  1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43 ve 47 olmak üzere 16 tane çıkar formülü kullanalım.

48 sayısı 

şeklinde çıkar.

Kümeler Alt Konular

Küme konusunun alt başlıkları:

Küme Kavramı
Kümelerin Gösterimi
Sonlu ve Sonsuz Kümeler
Alt Küme Kavramı
Denk ve Eşit Kümeler
Kümelerde Birleşim ve Kesişim
Evrensel Küme ve Bir Kümenin Tümleyeni
İki Kümenin Farkı
Küme Problemleri


Kümeler : Küme matematikteki tanımsız terimlerden biri olarak bilinir. Genel ifade olarak küme hakkında iyi tanımlanmış nesneler topluluğu denebilir. Küme oluşturulabilmesi için verilen ifadenin net ve anlaşılır halde olması gerekmektedir. Kümenin tanımıyla alakalı aşağıda verdiğimiz kavrama sorularını lütfen dikkatle inceleyiniz.

"Bir yıl içerisinde bulunan bahar ayları" ifadesinin küme belirtip belirtmediğini bulunuz.

"Bir yıl içerisinde bulunan bahar ayları" herkes tarafından aynı şekilde anlaşılır ve net bir ifade olduğundan  küme belirtir.
Kümenin elemanları Mart, Nisan ve Mayıs aylarıdır.
Cevap: Kümedir

"Son günlerdeki sorunlu olaylar" ifadesinin küme belirtip belirtmediğini bulunuz.
"Son günlerdeki sorunlu olaylar" ifadesindeki son günler netlik içermemekte ve belirsiz bir durumu ifade etmektedir.
Bundan dolayı ifade küme değildir. Cevap: Küme değil

"1 den küçük pozitif doğal sayılar" ifadesinin küme belirtip belirtmediğini bulunuz.

 "1 den küçük pozitif doğal sayılar"  ifadesini inceleyelim, burada 1 den küçük herhangi  bir pozitif doğal sayı olmamasına rağmen net ve anlaşılır olduğu için kümedir. Ancak bu kümenin elemanı yoktur.
Cevap: Kümedir

9. Sınıf Kümeler Çalışalım

1. Soru : “ KAZANMAK ” kelimesinin harflerinin oluşturduğu kümeyi C harfli ile isimlendirerek liste  ile gösteriniz. Eleman sayısını bulunuz.

Çözüm : C = {  K, A, Z, N, M }olup   s ( C )  =  5 olur yani C kümesinin eleman sayısı 5 tir.

2. Soru :  s ( A )  =  8 ise alt küme sayısını ve özalt küme sayısını bulunuz.

Çözüm : Alt küme sayısı : 2 üssü 8 = 256 olur. Öz alt küme sayısı : 2 üssü 8 - 1 = 256 - 1 = 255 olur.

3. Soru :  A = { a, b, c, d, 1, 2, 3 } ve B = { b, c, f, 3, 4, 5 } kümeleri için A∪B , A∩B , A-B, B-A kümelerini bulunuz.
Çözüm :
A∪B  = { a, b, c, d, 1, 2, 3, f, 4, 5 }
A∩B =  {  b, c, 3 }
A-B =  { a,  d, 1, 2 }
B-A =  { f, 4, 5 }

9. Sınıf Kümeler

      Küme, iyi tanımlanmış ögeler topluluğuna denir. Burada iyi tanımlanmış ifadesini biraz açalım. İyi tanımlanmış, herkes tarafından ilk duyulduğunda aynı şekilde anlaşılan objektif ifadelerdir. Geneli mantık konusunda olduğu gibi, kesin hüküm bildirmesidir.
     Örneğin, haftanın günleri, okulumuzun çalışkan öğrencileri, 5 ten büyük asal sayılar, bazı doğal sayılar ifadelerinin küme belirtip belirtmediğini inceleyelim. ilk ifade, haftanın günleri herkes tarafından aynı şeklide anlaşılır Pazartesi, Salı diye sayarak 7 tane kelime söyleriz yani bir küme belirtir. Küme, iyi bir şekilde tanımı yapılan öge topluluğudur.. İkinci ifade, okulumuzun çalışkan öğrencileri çalışkan kelimesinin net bir kıstası yoktur sana göre 50 alan başarılı sayılır bana göre 70 alan başarılı sayılır bu sebeple ikinci ifade küme belirtmez. Üçüncü ifade, 5 ten büyük asal sayılar bu soruyu 7, 11, 13 diye sayarız yani üçüncü ifade küme belirtir. Son ifade, bazı doğal sayılar cevap verirken kimi 1, 2, 3, 4, diye kimi 102, 336, 181 gibi sayıları söyleyebilir bu sebeple dördüncü ifade küme belirtmez.
       Bunun gibi, sevimli hayvanlar, güzel evler ifadeleri küme belirtmez. Küme, tanımı net olan öge topluluğudur.

9. Sınıf Matematik Müfredatı Aralık

Denklem ve eşitsizlikler ünitesinde sona doğru gelmekteyiz. Denklem kurma ile arası iyi olmayan denklem kurmayı bilmeyen öğrenciler için hafif düzeyde basit alıştırmalar önerilir.

 Denklem, Denklem Kurma, Denklem Çözme Eşitsizliklerle İlgili Uygulamalar

Denklem ve eşitsizlikleri gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır. Sözel ifadeleri sayısal terimlerle yazmak yani denkleme kurmak.

Denklem ve eşitsizlikleri gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır.
Sayı problemleri işlenir. Denklemi yazılır ve çözülür.

Denklem ve eşitsizlikleri gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır. Kesir problemleri işlenir. Denklemi yazılır ve çözülür.

Denklem ve eşitsizlikleri gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır.
Yaş problemleri işlenir. Denklemi yazılır ve çözülür.

Denklem ve eşitsizlikleri gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır.
İşçi - havuz problemleri işlenir. Denklemi yazılır ve çözülür.

Denklem ve eşitsizlikleri gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır. Yüzde problemleri işlenir. Denklemi yazılır ve çözülür.

9. Sınıf Matematik Müfredatı Kasım

Denklem ve eşitsizlikler ünitesinde ilerliyoruz. Denklem çözme ile arası iyi olmayan öğrenciler için hafif düzeyde basit alıştırmalar önerilir.


Son ünitenin 5. bölümü ile ünitede farklı bir kısma geçeceğiz.

 5. Birinci dereceden iki bilinmeyenli denklem ve eşitsizlik sistemlerinin çözüm kümelerini bulur

Mini bir değerlendirme yapılır.

 Üslü ifadeler

1. Üslü ifadeleri içeren denklemleri çözer.

Çıkmış sorular çözülür.

 Köklü İfadeler
1. Köklü ifadeler ve özelliklerini bir gerçek sayının rasyonel sayı kuvveti ile ilişkilendirerek açıklar.

Olimpiyat derecesine kadar sorular çözülür.

Oran Orantı
1. Oran ve orantı kavramlarını gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır.

Oran orantı konusu öğrencilerin en çok takıldığı konulardandır. Doğru orantı sindire sindire işlenmelidir. Ters orantı ve bileşik orantı konusu peşpeşe verilmelidir.

Denklem Kurma (Başlangıç) Problemleri

1. Denklem ve eşitsizlikleri gerçek / gerçekçi hayat durumlarını modellemede ve problem çözmede kullanır.

Kasım ayı ile dönemi ortalamış hatta ikinci bölüme kadar girmiş oluyoruz. Test yapma ve tek tek analiz yapma bir çok eksiklikleri fark etme açısından faydalıdır.

9. Sınıf Matematik Müfredatı Ekim

Kümeler ünitesinden sonra Denklem ve Eşitsizlikler ünitesine geçiyoruz. Denklem ile arası iyi olmayan öğrenciler için hafif düzeyde basit alıştırmalar önerilir.

Gerçek (Gerçel / Reel) Sayılar

1.İrrasyonel sayılar ve gerçek sayılar kümesini açıklar.
2 Gerçek sayılar kümesinde birinci dereceden eşitsizliğin özelliklerini açıklar.

Birinci Dereceden Denklem ve Eşitsizlikler

1. Gerçek sayılar kümesinde birinci dereceden eşitsizliğin özelliklerini açıklar.
2. Gerçek sayılar kümesinde aralık kavramını açıklar.
3. Birinci dereceden bir bilinmeyenli denklem ve eşitsizliklerin çözüm kümelerini bulur

Mutlak Değer

4. Bir gerçek sayının mutlak değeri ile ilgili özellikleri gösterir ve mutlak değerli ifade içeren birinci dereceden bir bilinmeyenli denklem ve eşitsizliklerin çözüm kümelerini bulur.

Ekim ayı sonunda birinci yazılı uygulama yapılacaktır. Ondan önce bir ünite değerlendirme iyi olur.

Dersburada, Özel Ders , Özel Eğitim

Dersburada.net kimdir?

Dersburada.net , '' eğitimde kalite '' parolası 2010 yılında, iki üniversite öğrenci tarafından bir proje kapsamında yola çıkmış, 2012 yılında hizmet vermeye başlamıştır. Dersburada.net başarıya ulaşmak adına çeşitli metotlar, psikolojik o ve mental açıdan en uygun ortamı sağlamaktadır. Bünyesinde bulunan, alanında uzman eğitmen kadrosu ile Dersburada.net eğitime bir nefes aldırmak adına yoluna emin adımlarla ilerlemektedir. Sadece metropol şehirler değil, Türkiye'nin tüm illerinde hizmet veren Dersburada.net ülkemizde eğitim ile ilgili eksiklikleri ve yanlışlıkları bilmekle beraber bunları düzeltecek sisteme ve alt yapıya sahiptir. Dersburada.net öğrencilerin eğitim hayatının düzenlenmesi ve daha sağlıklı bir gelecek için tüm öğrencilerin yanında ve hizmetindedir.

Özel Ders Nedir?

Zaman geçtikçe eğitim konusunda da değişimler meydana gelmektedir. Süre gelen eğitim sistemi bazı durumlarda yetersiz kalmakta ve insanları farklı arayışlara sürüklemektedir. Her ne kadar eğitim sürekli değişim yaşasa da özel ders sürekliliğini her zaman devam ettirecektir. Özel ders bu arayışta bir nevi can simidi konumundadır. Şüphesiz ki özel ders eğitim metotları içerisinde en çabuk reaksiyon alınan ve en etkili eğitim biçimidir. Öğrenci- öğretmen ilişkisi başarının anahtarıdır. Okuldaki veya bağlı bulunduğu eğitim kurumunda yeterli seviyeye ulaşamayan öğrenciler bu sistemle başarıya ulaşması işten bile değildir. Dersburada.net kapsamında bulunan deneyimli öğretmenler ile özel ders alabilir ve birçok branş da eksikleri gidermek çok kolay. Eğitmen konuyu derinlemesine ve en verimli şekilde öğrenciye aktarır, yanlışlıkları ve öğrencinin anlamadığı noktaları aydınlatır ve bu sayede öğrencinin başarıya ulaşmasına ön ayak olmaktadır. Özel ders aynı zamanda birçok olumsuz durumu da ortadan kaldırmaktadır, öğrencinin yaşayabileceği dikkat dağınıklığının eğitmen tarafından kontrol edilmesi ile maksimum verimde bir ders işlenmiş olur.

Sınavlara Hazırlıkta Özel Dersin Önemi

Ülkemizde bulunan mevcut eğitim sistemi rekabet ortamı ile paralel olarak öğrencilerin sınavlara hazırlamaktadır. Öğrencilerin bu sınavlara eksiksiz bir şekilde girmek ve istedikleri bölümlere, üniversitelere yerleşmek amacındalar. Öğrencilerin bu yolda en büyük destekleyicisi konumundaki sistem özel derstir. Peki, özel ders öğrencilerin sınavlara hazırlanmasında neden bu kadar etkin bir konumda?

Özel ders eğitmeni sınav sistemi hakkında her türlü bilgi birikimine sahiptir. Sınavlarda öğrencinin başına gelebilecek psikolojik ve bilgisel olumsuzlukları önceden tahmin edebilir ve bu konuda yol göstericidir. Sınavlarda her ne kadar bilgi önemli olsa da, test teknikleri, psikolojik durum da önemlidir. Eğitmen öğrencinin bu konudaki eksikliklerini yerinde tespit ve çeşitli yöntemlerle kapatır. Bu sayede öğrenci sınava hazırlıkta kendisini hem bilgi hem de psikolojik açıdan iyi hazırlar.

Dersburada.net ile kaliteli eğitime ulaşmak çok kolay. Siz de bize ulaşın ve size en uygun ve kaliteli eğitimi evinize kadar ulaştıralım.

9. Sınıf Matematik Müfredatı Eylül

2014 - 2015 Eğitim - Öğretim yılında 9. sınıf öğrencileri için hazırlanan Matematik dersinin Eylül ayı konularıdır.9. sınıf konuları ygs konuları olduğu için üzerinde özenle durulmalıdır.
Öğrenciyle tanışma.Ders müfredatının tanıtımı, matematik dersi için gerekli malzemeler, dersi anlama ve derse katılma ile ilgili görevler işlenir.

1. Bölüm :Küme Tanımı

1. Küme kavramını örneklerle açıklar ve kümeleri ifade etmek için farklı gösterimler kullanır.
2. Evrensel küme, boş küme, sonlu küme ve sonsuz küme kavramlarını örneklerle açıklar.
3. Alt küme kavramını ve özelliklerini açıklar.
4. İki kümenin eşitliğini açıklar.

Farklı kaynaklardan soru çözülür.

2. Bölüm : Kümelerde İşlemler

1. Kümelerin birleşim, kesişim, fark ve tümleme işlemlerini yapar; bu işlemler arasındaki ilişkileri ifade eder.
2. İki kümenin Kartezyen çarpımını açıklar.
3. Kümelerde işlemleri kullanarak problem çözer.

Farklı kaynaklardan soru çözülür.

Ünite değerlendirme testi yapılması yerinde olur.

Öğretmen bu Eylül ayında başarılı olursa çok iyi bir verim alır.

Diğer ayın konusuna iyi bir giriş için kümeler konusu tam anlaşılmalıdır.

10. Sınıf Matematik

       Milli Eğitim Bakanlığı 10. sınıf matematiğinde ciddi anlamda değişikliğe gitti . İlk olarak 4 saat matematik dersi zorunlu oldu. Geometri dersi ile matematik dersi birleşti. İkinci olarak matematik dersi ile geometri dersi birleşerek (4 + 2 = 6) 6 saat oldu ve zorunlu bir ders oldu. Daha önce 9. sınıflarda 4 saat matematik dersi zaten zorunlu idi ilk önce 2 saat geometri dersi de zorunlu olarak geldi birleştirildi (4 + 2 = 6) 6 saat oldu ve zorunlu bir ders oldu. Seneye 11. sınıflarda değişiklik yapılacak. Üniversite sınavına doğru 12. sınıflardaki değişiklikte 2016 da olacak.
     10. sınıf matematiğinde kazanımlar düştü böylelikle bir taraftan 10. sınıf matematiğinin zorluğu bir taraftan ülke genelinde 10. sınıf matematiğinde yapılan uygulamalar öğrencileri bir hayli yoracak.
     Öğrenciler özellikle basit kaynakları bitirmeli. Kartezyen eğitim kurumlarının turuncu seri fasikülleri en basitten almaktadır. Bu fasiküller öğrenciyi doyuracak kapasiteye sahiptir.
      Trigonometri çalışırken formülleri küçük kağıtlara not almaları faydalıdır. Ara ara tekrar etmeleri gerekir.

Denklem Tanımı

Bir ifade genel bilgi içerirse bu bilgidir. Tek sayılar 2 şer 2 şer azalır, sıfır sayı doğrusunun ortasında bulunur gibi. Bir eşitlik bilinmeyen içerirse buna denklem denir. Bilinmeyen bir tane ise bir bilinmeyenli denklem, bilinmeyen iki tane ise iki bilinmeyenli denklem denir. Bu bilinmeyen x, y, a, b, veya m olabilir yani adı sanı önemli değildir. Örneğin, 2x + 4 = 12 3y + 5 = 17, 4a  - 1 = 15 ifadeleri birinci dereceden bir bilinmeyenli denklemlerdir. Çözümlerini ele alalım.

2x + 4 = 12 önce + 4 ü karşıya - 4 olarak geçirelim.
2x = 12 - 4  çıkarma yapalım.
2x = 8 şimdi her iki tarafı 2 ile bölelim.
x = 8/2
x = 4

yani 2x + 4 = 12 birinci dereceden bir bilinmeyenli denklemin kökü 4 olur.

3y + 5 = 17 önce + 5 ü karşıya - 5 olarak geçirelim.
3y = 17 - 5  çıkarma yapalım.
3y = 12 şimdi her iki tarafı 3 ile bölelim.
y = 12/3
y = 4

yani 3y + 5 = 17 birinci dereceden bir bilinmeyenli denklemin kökü 4 olur.

Mutlak Değerde Kafes Yöntemi

Mutlak değerli denklem sorularında eşitsizlik soru modelinde hem eşitsizlik hem denklem hem de mutlak değer konularının kesişimi olan bir soru modeli vardır. Bu model aslında en uzun çözümü içeren modeldir.

Bu soru üzerinde yöntemi biraz irdeleyelim.
mutlak x + mutlak y < 3 olsun.  Burada
mutlak x + mutlak y = 0,
mutlak x + mutlak y = 1 ve
mutlak x + mutlak y = 2 durumlarını inceleyelim.

mutlak x + mutlak y = 0 de x= ve y= 0 olur.
mutlak x + mutlak y = 1 de 2 durum vardır.

mutlak x = 1 ve  mutlak y = 0 ise x, 1 ya da -1 ; y ise 0
mutlak x = 0  ve  mutlak y = 1 ise y, 1 ya da -1 ; x ise 0

mutlak x + mutlak y = 2 de 3 durum vardır.
mutlak x = 2 ve  mutlak y = 0 ise x, 2 ya da -2 ; y ise 0
mutlak x = 0  ve  mutlak y = 2 ise y, 2 ya da -2 ; x ise 0
mutlak x = 1 ve  mutlak y = 1 ise x, 1 ya da -1 ; y ise 1 ya da -1

Ygs Karışım sorusu

Bir konuya çalışırken soru analizi konuyu öğrenmede etkili bir öğrenme metodudur. Konuya ait bir soru üzerinde yazarak  yorum yapmak yazıya dökmek o soru ile ilgili  orijinal yeni çıkabilecek sorulara da bir ön hazırlık demektir. Anahtar kelime yazarak çalışmaktır. Karışım soruları şekil çizilirse daha kolay çözüme gidilir. Çıkmış sorulara bakarsak sayı olarak tek tük çıktığını görürsünüz. Ygs karışım sorusu sadece ygs sınavında değil lys sınavında ales sınavında kpss sınavında ve dgs sınavında da çıkmaktadır.

Ygs matematik içerisinde karışım soruları denklem kurma soruları içinde en son bölümde yer alır. Mantığı kolay olup şekil çizerek kap çizerek çok çabuk çözüme gidilir.

Bir soru çözelim. Soru yukarıdaki resimde olup oldukça açık yazılmıştır. Soruda alınan miktar düşülüp yine aynı miktar konduğu için aslında ağırlı değişmemektedir.

Yapmanız gerekn soruyu bir de kendiniz çözmenizdir. Pratik zamanla olur. Pratik olmak için çalışma ve özellikle yazmak lazım.

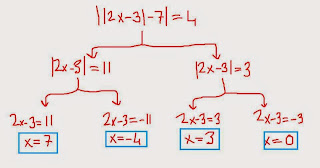
Ygs Mutlak Değer Çözümü

Ygs matematik konularından mutlak değer konusu çok keyifli bir konudur. Bu konu bazı soruları bol denklem içerir. Vereceğimiz soruda çözüm kümesi adeta bize denklem çözme pratiği yaptıracaktır.
Soruyu analiz edelim.
İçiçe iki mutlak değer vardır. Neyden 7 çıkarırsak 4 ya da - 4 olur diye düşünmemiz lazım.
Bu sayılar 11 ile 3 olur.
Şimdi denkleme geçebiliriz.
Hangi sayının 2 katının 3 eksiği 11 ya da -11 ile 3 ya da - 3 olur diye düşünerek tam 4 tane denklem çözmek mutlak değer çözmek oluyor.

2x - 3 = 11 denkleminde x değeri 7 olur. 

2x - 3 =  - 11 denkleminde x değeri  - 4 olur. 

2x - 3 =  3 denkleminde x değeri 3 olur. 

2x - 3 =  - 3  denkleminde x değeri 0 olur. 

Böylece denklemim çözüm kümesi olarak 7 , - 4 , 3 , 0 olarak 4 tane değer çıkar.

Matematikte Haftalık Tekrar

        Matematikte haftalık tekrar tekrar olmadığı sürece, çalıştıklarınızın çoğu boşa gider ve siz elinizde kalan üç beş netle , küçük kısım sayesinde başarıyı yakalamaya uğraşacaksınız. Günde on saat çalışıp, iki saat çalışmış kadar başarı elde edersiniz. Başarılarınızın tam olarak karşılığını alabilmek istifade edebilmek için; tekrarları ihmal etmeyiniz. Tekrar yapınız.

       Düzenli olarak tekrar yapacağınız günlük tekrar ile bilgilerinizin çoğunu taze tutmuş olursunuz. Haftalık yapacağınız matematik tekrarı ise; günlük tekrarınızdan daha kapsamlı olacak ve arada unuttuğunuz bazı bilgileri toptan tazelemenizi sağlayacaktır.

         Haftalık tekrar ederken, bütün matematik notlarınızı birer kere en baştan itibaren okuyun. Matematik dersinden yapamadığınız ve çözümünü öğretmenlerinizden sorarak öğrenmiş olduğunuz tüm soruları saklayın, haftalık tekrarlarınızda bu çözümlü sorular bu soruların üzerinden geçin. Son olarak da, mutlaka her tekrarını yapmış olduğunuz konudan en az on - yirmi soru çözün. Bunun için kendinize soru bankaları ile tekrar kaynakları edinebilirsiniz.

            Her konuya ait 5 testi olan bir kaynak, sizin 3 aylık tekrarınız için yeterli olacaktır. Haftalık matematik tekrarınızı yapmak için, ille de haftanın bir gününü mesela Çarşamba yalnızca tekrar için ayırın. Bu günü hiç bir programla mümkün ise; sade seçim. O  günü yoğun bir temponuz var ise; dilerseniz Pazar farklı bir gün de olabilir. Tekrar gününüzde, tek ders için tekrardan başka farklı bir ders çalışmayın. Yalnızca matematik tekrarınızı yapın ve mümkünse hafif bir çalışma temposu içerisinde, elinize bir miktar şeker ile enerji deposu yapın  sonraki günler için enerji depolayın. Ders esnasında işinizi kolaylaştırır.